bernitro.blogg.se

#includeĬout= 0.01) //tell about interval is sufficently smallĬout<<"The value of root is = "<f(a) and f(c) have opposite signs or f(b) and f(c) have opposite signs.Either f(c)=0 then we can stop directly as c will be itself the root.At each step divide the interval into halves c=a+b/2 and find the value of f(c).

If we have a closer look into the function 'f' we can easily notice there are very limited set of values for which it will evaluated to. By intermediate value theorem, there must exist one root that lies between (a,b). You need to define 'f' as anonymous function and 'f' should hold the handle of the function as below: > f (p)600p4-550p3+200p2-20p-1 II. As and are on opposite sides of the x-axis, the solution at which must reside somewhere in.

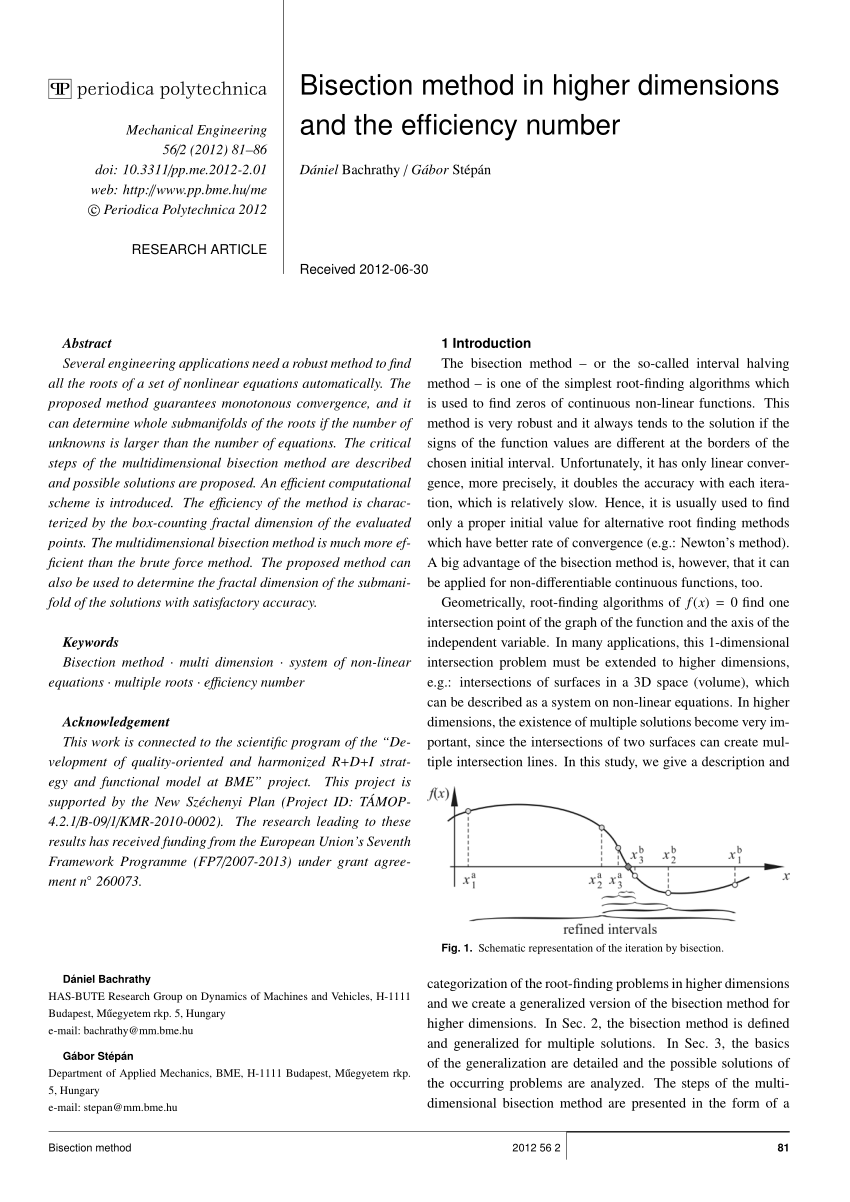
This method requires two initial guesses satisfying. Let f(x) be a function in an interval, where f is continuous and f(a) and f(b) have opposite signs. Given a value of oxygen con centration, this formula and the bisection method can be used to solve for temperature in C. Here we consider a set of methods that find the solution of a single-variable nonlinear equation, by searching iteratively through a neighborhood of the domain, in which is known to be located. This method is also called interval halving method, binary search method, or dichotomy method. It is a very simple and robust method, but relatively slow. The method involves repeatedly bisecting of the interval and ultimately reaching to the desired root. This method is used to find roots in a continuous function between two given interval, given the two values to be in the opposite signs. In this tutorial, we are going to learn about the implementation of the bisection method in C++.